完整鍊和鏈節的歐姆定律：公式選項、描述和解釋

對於閉路

閉合電路是指電流循環通過的閉合電氣連接。當有一系列電線相互連接並完成電路時，我從圓的一端跑到另一端，這將是一個閉合電路。

EMF (E) - 以伏特表示和測量，是指根據法拉第定律由電池或磁力產生的電壓，該定律指出時變磁場會感應出電流。

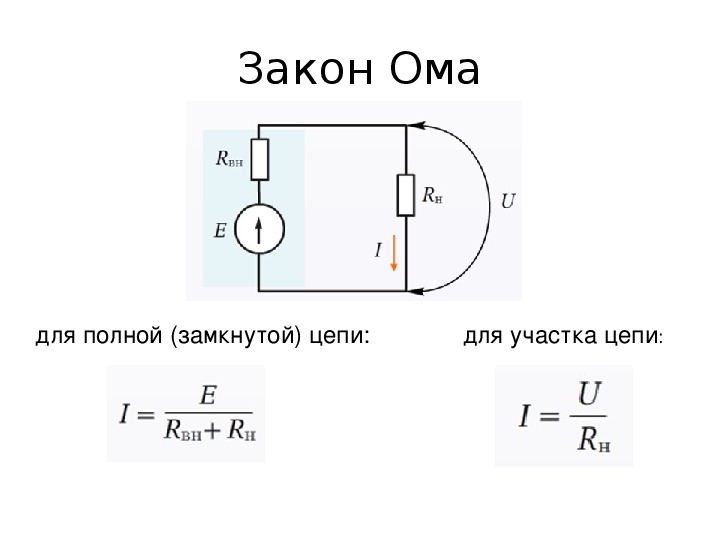
那麼：E = IR + Ir

E \u003d I (R + r)

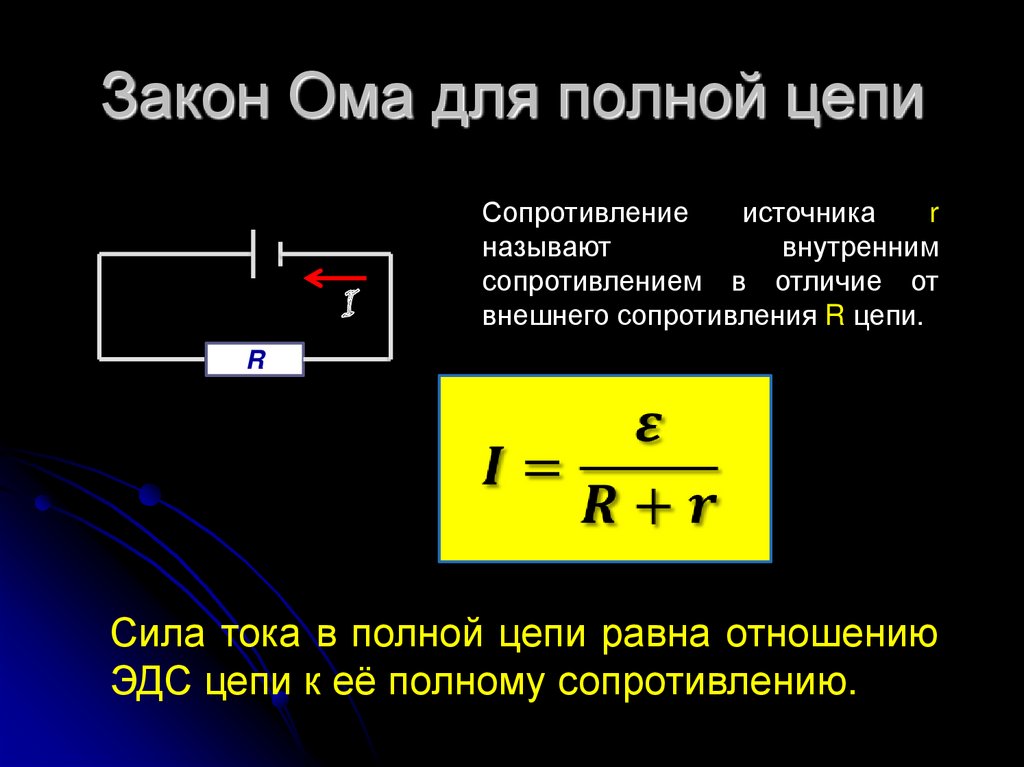
我 \u003d E / (R + r)

其中： r 是電流源的電阻。

這個表達式被稱為歐姆閉環電路定律。

異構鏈

獨立的部分和完整的電路

應用於部分或整個電路的歐姆定律可以在兩個計算選項中考慮：

• 單獨的短節。它是沒有 EMF 源的電路的一部分。
• 由一個或多個部分組成的完整鏈。這還包括一個具有自身內部電阻的 EMF 源。

電路電流部分的計算

在這種情況下，應用基本公式 I \u003d U / R，其中 I 是電流強度，U 是電壓，R 是電阻。據此，可以製定出普遍接受的歐姆定律解釋：

這個公式是平面設計中所謂的“洋甘菊”上許多其他公式的基礎。在扇區 P - 確定功率，在扇區 I、U 和 R - 執行與電流強度、電壓和電阻相關的動作。

每個表達式 - 基本的和附加的，都允許您計算電路中使用的元件的確切參數。

使用電路的專家使用圖中所示的三角形方法快速確定任何參數。

計算應考慮連接部分元件的導體的電阻。由於它們由不同的材料製成，因此此參數在每種情況下都會有所不同。如果需要組成一個完整的電路，那麼在主公式中補充一個電壓源的參數，例如，一個電池。

完整鏈的計算選項

完整的電路由各個部分組成，並與電壓源 (EMF) 組合成一個整體。因此，這些部分的現有電阻由連接源的內部電阻補充。因此，前面討論的主要解釋如下：I = U / (R + r)。此處，已添加 EMF 源的電阻指示器 (r)。

從純物理學的角度來看，這個指標被認為是一個很小的值。然而，在實踐中，在計算複雜的電路和電路時，專家們不得不將其考慮在內，因為額外的阻力會影響工作的準確性。此外，每個源的結構非常不均勻，因此，在某些情況下，電阻可以用相當高的比率來表示。

上述計算是針對直流電路進行的。交流電的動作和計算是根據不同的方案進行的。

法律對變量的影響

用交流電，電路的電阻就是所謂的阻抗，由有源電阻和無功電阻負載組成。這是由於存在具有電感特性和正弦電流值的元件。電壓也是一個變量，根據其自身的開關規律起作用。

因此，計算歐姆定律交流電路設計時要考慮到特定影響：電壓電流幅度的超前或滯後，以及有功和無功功率的存在。反過來，電抗包括電感或電容分量。

所有這些現象將對應於公式 Z \u003d U / I 或 Z \u003d R + J * (XL - XC)，其中 Z 是阻抗； R——有功負載； XL、XC——感性和容性負載； J 是校正因子。

完整電路中的 EMF 源

對於閉合電路中電流的發生，該電路必須包含至少一個特殊元件，其中將發生其兩極之間的電荷轉移工作。在該元素內攜帶電荷的力是對抗電場的，這意味著它們的性質必須不同於電場。因此，這種力量被稱為第三方。

米。 1. 物理學中的外力。

電路中的一種元件，其中外力起作用以抵抗電場的作用轉移電荷，稱為電流源。它的主要特徵是外力的大小。為了表徵它，引入了一個特殊的度量 - 電動勢 (EMF)，它用字母 $\mathscr{E}$ 表示。

電流源的 EMF 值等於電荷轉移的外力與該電荷值的比值：

$$\mathscr{E}={A_{st}\over q}$$

由於 EMF 的含義與電壓的含義非常接近（回想一下，電壓是攜帶電荷的電場所做的功與該電荷值的比值），因此 EMF 與電壓一樣，以伏特：

$$1B={J\overCl}$$

實際電流源的第二個最重要的電氣特性是其內部電阻。當電荷在端子之間轉移時，它們與 EMF 源的物質相互作用，因此，電流源也存在一定的電阻。內阻與普通電阻一樣，以歐姆為單位，但用小寫拉丁字母 $r$ 表示。

米。 2. 電流源示例。

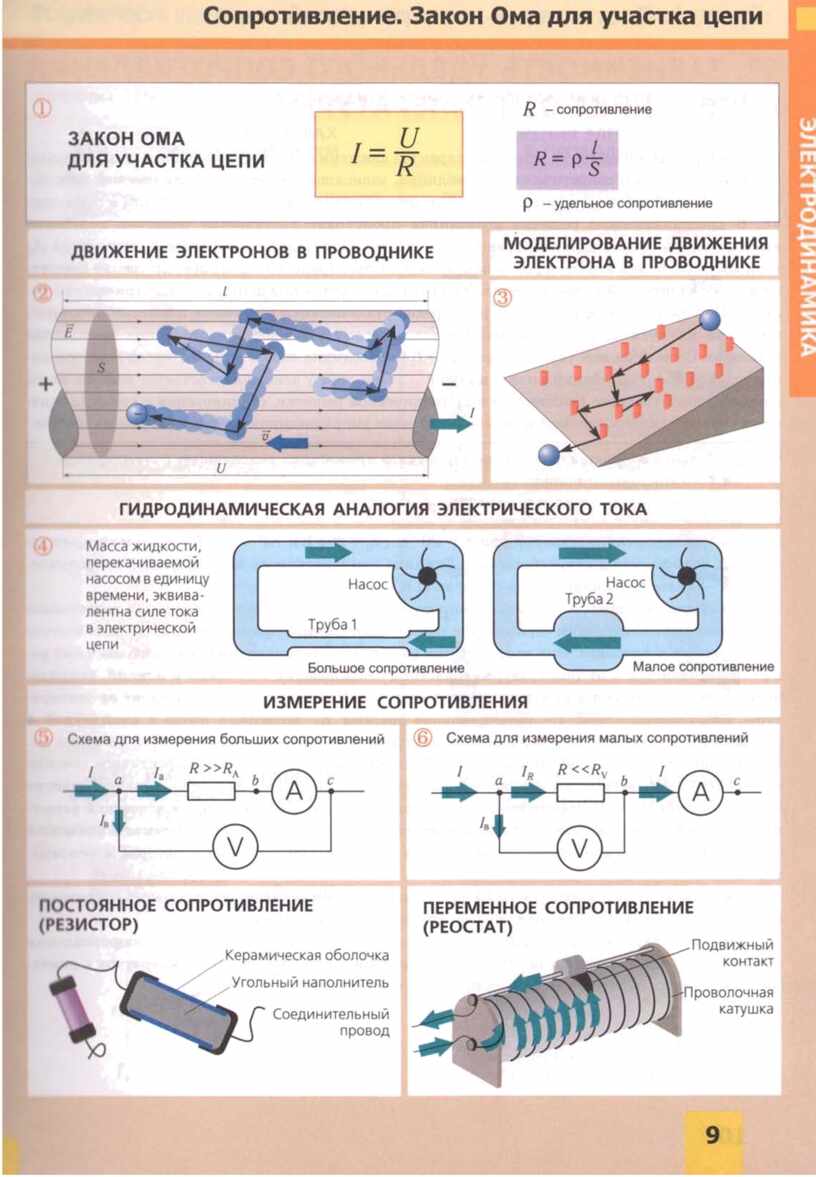
R - 電阻

電阻是電壓的倒數，可以將其與在流水中移動物體的效果進行比較。 R 的單位是 Om，用大寫的希臘字母 Omega 表示。

電阻的倒數 (1/R) 稱為電導率，它衡量物體傳導電荷的能力，以西門子單位表示。

使用的幾何獨立量稱為電阻率，通常用希臘符號 r 表示。

附加信息。歐姆定律有助於建立電網運行的三個重要指標，從而簡化了功率的計算。不適用於具有二極管、晶體管等元件的單面網絡。並且它也不適用於非線性元件，例如晶閘管，因為這些元件的電阻值隨著不同的給定電壓和電流而變化。

在較高頻率下，分佈式行為變得占主導地位。很長的電源線也會發生同樣的情況。即使在低至 60 Hz 的頻率下，很長的傳輸線（例如 30 公里）也具有分佈式特性。主要原因是電路中傳播的有效電信號是電磁波，而不是電壓和電流，它們會被電磁波感染。導體只是充當波的嚮導。因此，例如，同軸電纜將顯示 Z = 75 歐姆，即使其直流電阻可以忽略不計。

歐姆定律是電氣工程的基本定律。它在所有電路和電子元件中都有大量的實際應用。

應用歐姆定律最常見的例子：

1. 提供給電加熱器的電源。給定加熱器線圈的電阻和施加的電壓，可以計算提供給該加熱器的功率。
2. 保險絲的選擇。它們是與電子設備串聯的保護元件。保險絲/斷路器的額定電流為安培。電流保險絲額定值是使用歐姆定律計算的。
3. 電子設備的設計。筆記本電腦和手機等電子設備需要具有特定額定電流的直流電源。典型的手機電池需要0.7-1A，一個電阻用來控制流過這些元件的電流速率。歐姆定律用於計算典型電路中的額定電流。

曾幾何時，歐姆的結論成為電力領域新研究的催化劑，今天它們並沒有失去意義，因為現代電氣工程就是基於它們。 1841年，歐姆被授予英國皇家學會最高榮譽科普利勳章，“歐姆”一詞早在1872年就被公認為抵抗單位。

直流電路的非均勻部分

異質結構具有這樣的電路部分，除了導體和元件之外，還有一個電流源。在計算該區域的總電流強度時，必須考慮其 EMF。

有一個公式定義了異構站點的主要參數和過程：q = q0 x n x V。其指標表徵如下：

• 在移動電荷（q）的過程中，它們獲得了一定的密度。其性能取決於電流強度和導體的截面積（S）。
• 在一定濃度（n）的條件下，可以準確地表示在單個時間段內移動的單位電荷數（q0）。
• 對於計算，有條件地將導體視為具有一定體積 (V) 的圓柱形截面。

將導體連接到電池時，電池會在一段時間後放電。也就是說，電子的運動逐漸減慢，最終完全停止。導體的分子晶格促進了這一點，它抵消了電子之間的碰撞和其他因素。為了克服這種阻力，必須額外施加某些第三方力量。

在計算過程中，這些力被添加到庫侖力上。此外，為了將單位電荷 q 從第 1 點轉移到第 2 點，需要執行工作 A1-2 或簡單地執行 A12。為此，創建了一個電位差 (φ1 - φ2)。在直流電源的作用下，會產生 EMF，沿電路移動電荷。總應力的大小將由上述所有力組成。

在計算中必須考慮到直流電源連接的極性。當端子改變時，EMF 也會改變，加速或減慢電荷的運動。

元件的串聯和並聯

對於電路的元件（電路的一部分），特徵矩是串聯或併聯連接。

因此，每種類型的連接都伴隨著電流和電壓供應的不同性質。因此，歐姆定律也以不同的方式應用，具體取決於包含元素的選項。

一串串聯的電阻元件

對於串聯連接（具有兩個組件的電路部分），使用以下措辭：

• 我 = 我₁ = 我₂ ;
• U = U₁ + U₂ ;
• R=R₁ + R₂

這個公式清楚地表明，無論串聯連接的電阻元件的數量如何，在電路的一部分中流動的電流都不會改變值。

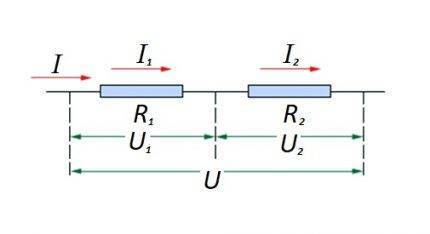將電路部分中的電阻元件彼此串聯連接。這個選項有它自己的計算規律。圖中：I、I1、I2——電流； R1、R2——電阻元件； U, U1, U2 - 施加電壓

施加到電路有源電阻元件上的電壓量是總和，並加起來就是 EMF 源的值。

在這種情況下，每個單獨組件上的電壓為：Ux = I * Rx。

總電阻應該被認為是電路所有電阻元件的值的總和。

一串並聯的電阻元件

在電阻元件並聯的情況下，根據德國物理學家歐姆定律，該公式被認為是公平的：

• 我 = 我₁ + 我₂ … ;
• U = U₁ = U₂ … ;
• 1/R = 1/R₁ + 1 / R₂ + …

當使用並行和串行連接時，不排除編譯“混合”類型的電路部分的選項。

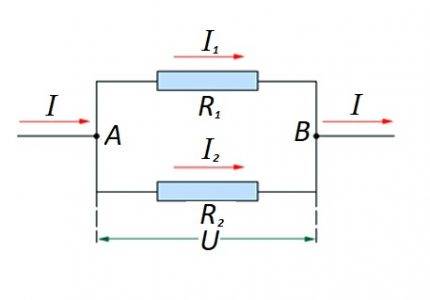電路部分中電阻元件相互並聯的連接。對於此選項，應用其自身的計算法則。圖中：I、I1、I2——電流； R1、R2——電阻元件； U——外加電壓； A, B - 進入/退出點

對於此類選項，通常通過並聯電阻額定值的初始計算來進行計算。然後將串聯電阻的值添加到結果中。

法律的積分形式和微分形式

上述所有計算要點都適用於“均質”結構的導體（可以說是電路的一部分）的情況。

同時，在實踐中，人們經常需要處理原理圖的構建，其中導體的結構在不同區域會發生變化。例如，使用較大橫截面的線材，或者相反，使用基於不同材料製成的較小的線材。

為了考慮到這種差異，所謂的“微分-積分歐姆定律”有一個變體。對於無限小的導體，電流密度水平的計算取決於強度和電導率值。

微分計算下，取公式：J = ό * E

對於積分計算，分別有公式：I * R = φ1 - φ2 + έ

然而，這些例子更接近高等數學學校，並沒有真正用於簡單電工的實際實踐中。

了解電流和電阻

讓我們從電流的概念開始。簡而言之，與金屬有關的電流是電子（帶負電的粒子）的定向運動。它們通常表示為小圓圈。在平靜的狀態下，它們隨意移動，不斷改變方向。在某些條件下——出現電位差——這些粒子開始向某個方向進行某種運動。這種運動就是電流。

為了更清楚，我們可以將電子與灑在某個平面上的水進行比較。只要飛機靜止，水就不會移動。但是，一旦出現斜坡（出現電位差），水就開始移動。電子也是如此。

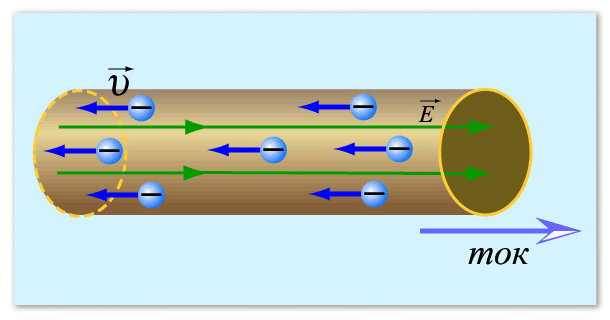
這就是可以想像電流的方式

現在我們需要了解電阻是什麼以及為什麼它們會與電流強度一起反饋：電阻越高，電流越低。如您所知，電子在導體中移動。通常這些是金屬線，因為金屬具有良好的導電能力。我們知道，金屬具有緻密的晶格：許多粒子緊密且相互連接。電子在金屬原子之間穿行，與它們發生碰撞，這使得它們難以移動。這有助於說明導體施加的電阻。現在很清楚為什麼電阻越高，電流強度越低——粒子越多，電子越難越過路徑，它們越慢。這似乎已經解決了。

如果您希望通過經驗測試這種依賴性，請找到一個可變電阻器，串聯一個電阻器 - 一個電流表 - 一個電流源（電池）。還希望在電路中插入一個開關——一個普通的撥動開關。

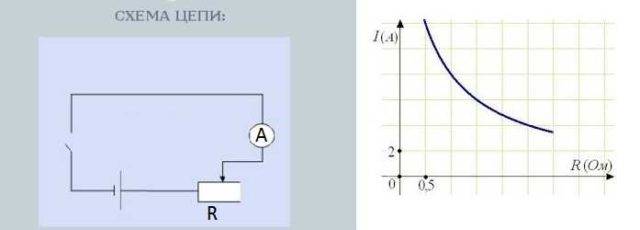
測試電流對電阻的依賴性的電路

轉動電阻旋鈕會改變電阻。同時，測量電流強度的電流表上的讀數也會發生變化。此外，電阻越大，箭頭偏離越小——電流越小。電阻越低，箭頭偏離越大 - 電流越大。

電流對電阻的依賴性幾乎是線性的，也就是說，它在圖形上反映為幾乎是一條直線。為什麼幾乎 - 這應該單獨討論，但這是另一個故事。

交流電的歐姆定律

在計算交流電路時，沒有引入電阻的概念，而是引入了“阻抗”的概念。阻抗用字母 Z 表示，它包括負載 R 的有源電阻_一個 和電抗 X （或 R_r）。這是由於正弦電流（和任何其他形式的電流）的形狀和電感元件的參數，以及開關定律：

1. 感應電路中的電流不能立即改變。
2. 具有電容的電路中的電壓不能立即改變。

因此，電流開始滯後或超前電壓，視在功率分為有功和無功。

U=I/Z

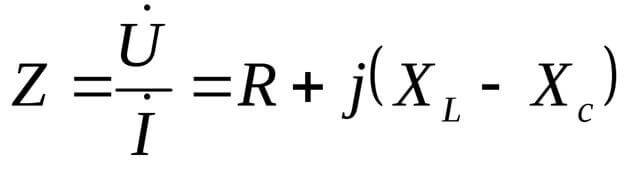
X_大號 和 X_C 是負載的無功分量。

對此，引入值 cosФ：

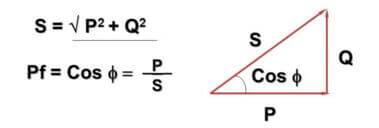
這裡 - Q - 由交流電和感容元件引起的無功功率，P - 有功功率（消耗在有源元件中），S - 視在功率，cosФ - 功率因數。

您可能已經註意到，該公式及其表示與勾股定理相交。這是真的，角度 Ф 取決於負載的無功分量有多大——它越大，它就越大。在實踐中，這導致實際流入網絡的電流大於家用電錶計入的電流，而企業則為全電付費。

在這種情況下，阻力以復數形式呈現：

這裡 j 是一個虛數單位，對於復雜形式的方程來說是典型的。不常稱為 i，但在電氣工程中，也表示交流電的有效值，因此，為了不混淆，最好使用 j。

虛數單位是√-1。平方時沒有這樣的數字是合乎邏輯的，這可能導致“-1”的否定結果。

當歐姆定律發生時

創造理想條件並不容易。即使在純導體中，電阻也會隨溫度而變化。它的減少使晶格分子的活動最小化，從而簡化了自由電荷的運動。在一定程度的“凍結”下，就會出現超導效應。加熱時觀察到相反的效果（導電性降低）。

同時，無論電流密度如何，電解質、金屬和某些類型的陶瓷都會保持電阻。參數的穩定性同時保持一定的溫度範圍使得可以應用歐姆定律的公式而無需額外的校正。

半導體材料和氣體的特點是電阻變化。該參數受控制體積中的電流強度顯著影響。為了計算性能特徵，必須應用專門的計算方法。

如果考慮交流電，則修正計算方法。在這種情況下，必須考慮反應成分的存在。由於電阻的電阻性質，可以應用基於歐姆定律公式的考慮計算技術。

基爾霍夫定律。

分配
電路分支中的電流
服從基爾霍夫第一定律，
以及截面上的應力分佈
鏈服從基爾霍夫第二定律。

基爾霍夫定律
與歐姆定律一起是主要的
在電路理論中。

首先
基爾霍夫定律：

代數
節點中的電流總和為零：

_一世
= 0 (19)

在哪裡
一世
是在給定節點收斂的分支數。

也就是求和
延伸到樹枝中的水流，
收斂於所考慮的
節點。

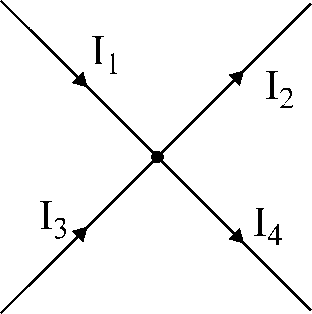
圖 17。插圖
基爾霍夫第一定律。

數字
根據第一個編制的方程
基爾霍夫定律由以下公式確定：

努普
= 怒
– 1,

在哪裡
怒
是考慮的鏈中的節點數。

電流跡象
方程被考慮到所選擇的
積極的方向。標誌在
如果電流相同，則電流相同
相對於此
節點。

例如，
對於圖 17 中所示的節點：
我們為流向節點的電流分配符號
“+”，以及從節點流出的電流 - 標誌
«-».

那麼方程
根據基爾霍夫第一定律，它會寫成
所以：

我₁
- 我₂
+ 我₃
- 我₄
= 0.

方程，
根據基爾霍夫第一定律編譯，
稱為節點。

這個
定律表達了這樣一個事實，即在節點
電荷不積累
並且不被消耗。電量
來到現場的費用等於總和
使節點保持一致的電荷
相同的時間跨度。

第二
基爾霍夫定律：

代數
電動勢之和在任何閉合電路中
鍊等於瀑布的代數和
該電路元件上的電壓：

Ui
= 
艾

IiRi=Ei(20)

在哪裡
一世
- 元素編號（電阻或
電壓源）在考慮
輪廓。

**數字
根據第二個編制的方程
基爾霍夫定律由以下公式確定：

努普
=鈮
- 怒
+ 1 – 內德斯。

在哪裡
鈮
- 電路的分支數量；

怒
——節點數；

內德
是理想電動勢源的數量。

圖 18。插圖
基爾霍夫第二定律。

為了，
正確寫出第二定律
給定輪廓的基爾霍夫，如下
遵守以下規則：

1. 任意
   選擇輪廓旁路的方向，
   例如，順時針（圖 18）。

2. 電動勢
   和匹配的電壓降
   在與所選方向的方向
   繞過寫在一個表達式中
   符號“+”；如果 e.f.s.和電壓降
   方向不匹配
   輪廓，然後它們前面有一個符號
   «-».

例如，
對於圖 18 的輪廓，基爾霍夫第二定律
會寫成如下：

ü₁
- 你₂
+ U₃
=E₁
– E₃
– E₄
(21)

等式（20）可以是
改寫為：

 (Ui
– Ei)
= 0 (22)

在哪裡
（U
– E)
- 樹枝上的張力。

最後，
基爾霍夫第二定律可以表述為
通過以下方式：

代數
在任何分支上的電壓總和
閉環為零。

潛在的
前面討論的圖表服務於
第二個圖形解釋
基爾霍夫定律。

任務編號 1。

在
圖 1 中的電路給定電流 I₁
和我₃,
電阻和電動勢確定電流
我₄,
我₅,
我₆
; a 點間電壓
和 b
如果我₁
= 10毫安，
我₃
= -20 毫安，
R₄
= 5kOhm,
乙₅
= 20B,
R₅
= 3kOhm,
乙₆
= 40B,
R₆
= 2kΩ。

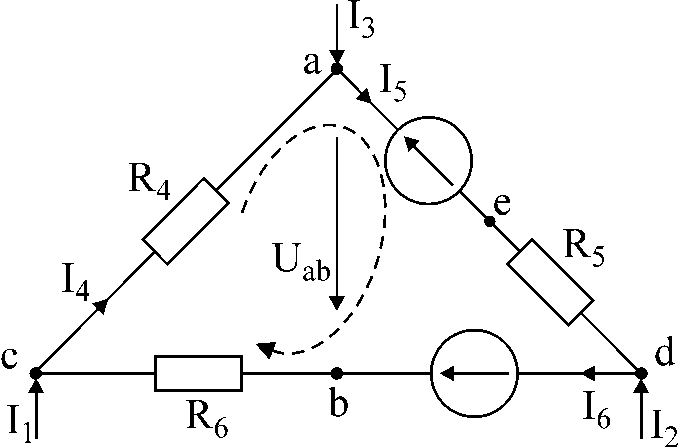
圖。1

解決方案：

1. 對於給定的
   輪廓，我們組成兩個方程根據
   基爾霍夫第一定律和一個 - 根據
   第二。輪廓方向
   用箭頭表示。

在
作為我們得到的解決方案的結果：我₆
= 0;我₄
= 10毫安；
我₅
= -10毫安

1. 問
   點間電壓方向
   一個
   和 b
   從點“a”
   指向“b”
   — 你_抗體.
   這個電壓可以從等式中找到
   基爾霍夫第二定律：

我₄R₄
+ U_抗體
+ 我₆R₆
= 0

ü_抗體
= - 50V。

任務編號 2。

為了
圖 2 中的圖表根據
基爾霍夫定律和確定未知數
點。

鑑於：
我₁
= 20毫安；
我₂
= 10毫安

R₁
= 5kOhm,
R₃
= 4kOhm,
R₄
= 6kOhm,
R₅
= 2kOhm,
R₆
= 4kΩ。

圖2

解決方案：

節點數
equations - 3、等高線方程的數量
– 1.

記住！
根據第二個編譯方程時
基爾霍夫定律，我們選擇輪廓，在
其中不包括當前來源。
輪廓的方向如圖所示。

在
在這個電路中，支路的電流 I₁
和我₂.
未知
電流
我₃,
我₄,
我₅,
我₆.

決定
系統，我們得到：我₃
= 13.75 毫安；
我₄
= -3.75毫安；
我₅
= 6.25毫安；
我₆
= 16.25毫安。

基本概念

當閉合電路允許電子從高電位移動到電路中的低電位時，電流就會流動。換句話說，電流需要一個具有使它們運動的能量的電子源，以及它們返回負電荷的點，其特點是它們的缺陷。作為一種物理現象，電路中的電流具有三個基本量的特徵：

• 電壓;
• 電流強度；
• 電子移動通過的導體的電阻。

力量和張力

電流強度（I，以安培為單位）是每單位時間通過電路中某個位置的電子（電荷）的體積。換句話說，測量 I 是確定運動中的電子數

重要的是要了解該術語僅指運動：例如，未連接電池端子上的靜電荷沒有可測量的 I 值。沿一個方向流動的電流稱為直流 (DC)，並且週期性變化的方向稱為交替（AC）。電壓可以用壓力等現象來說明，也可以用物體在重力影響下的勢能差來說明

為了製造這種不平衡，你必須首先消耗能量，這將在適當的情況下在運動中實現。例如，在負載從高處墜落時，需要做功以將其抬起，在原電池中，由於化學能的轉換，在端子處形成電位差，在發電機中 - 由於暴露於電磁場

應力可以用壓力等現象來說明，也可以用物體在重力影響下的勢能差來說明。為了製造這種不平衡，你必須首先消耗能量，這將在適當的情況下在運動中實現。例如，在負載從高處墜落時，實現了提升它的工作，在原電池中，由於化學能的轉換，在端子處形成電位差，在發電機中 - 由於暴露於電磁場。

導體電阻

無論普通導體有多好，它都不會允許電子在沒有運動阻力的情況下通過。可以將阻力視為機械摩擦的類似物，儘管這種比較並不完美。當電流流過導體時，一些電位差會轉化為熱量，因此電阻兩端總會有電壓降。電加熱器、吹風機和其他類似設備僅設計用於以熱量的形式耗散電能。

簡化電阻（表示為 R）是衡量電子流在電路中延遲多少的量度。它以歐姆為單位。電阻器或其他元件的電導率由兩個屬性決定：

• 幾何學;
• 材料。

形狀至關重要，從水力類比中可以看出：將水推過細長的管道比將水推過又短又寬的管道要困難得多。材料起著決定性的作用。例如，電子可以在銅線中自由移動，但根本不能流過橡膠等絕緣體，無論其形狀如何。除了幾何形狀和材料外，還有其他因素會影響電導率。

歐姆定律解釋

為確保電荷的移動，您需要關閉電路。在沒有額外電源的情況下，電流不能長期存在。潛力將很快變得平等。為了維持電路的工作模式，需要一個額外的電源（發電機、電池）。

完整的電路將包含所有組件的總電阻。為了準確計算，導體、電阻元件和電源的損耗都被考慮在內。

對於一定的電流強度，需要施加多少電壓，按以下公式計算：

U=I*R。

類似地，在所考慮的關係的幫助下，電路的其他參數被確定。

並行和串行連接

在電氣中，元件串聯連接 - 一個接一個，或併聯 - 這是當多個輸入連接到一個點，並且來自相同元件的輸出連接到另一個時。

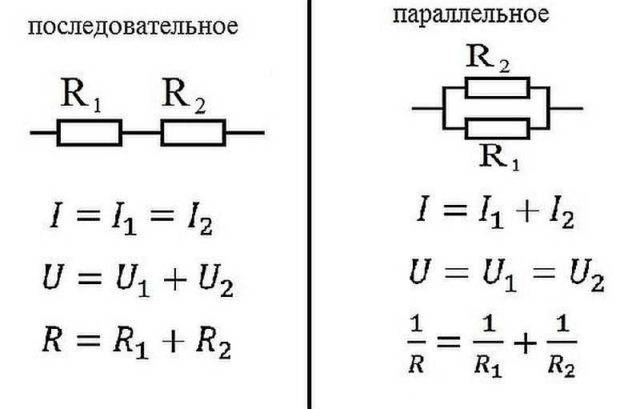
並聯和串聯連接的歐姆定律

串行連接

歐姆定律如何適用於這些情況？當串聯時，流過元件鏈的電流將是相同的。具有串聯連接的元件的電路部分的電壓計算為每個部分中的電壓之和。這怎麼解釋？電流通過元件的流動是將部分電荷從元件的一部分轉移到另一部分。我的意思是，這是一些工作。這項工作的重要性是緊張。這就是壓力的物理意義。如果這很清楚，我們繼續前進。

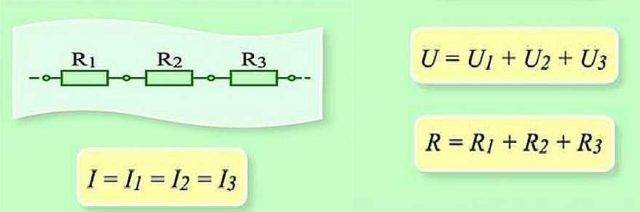
此段電路的串聯及參數

當串聯時，需要依次通過每個元件轉移電荷。在每個元素上，這都是一定的“工作量”。要找到整個鏈條部分的工作量，您需要添加每個元素的工作量。所以事實證明，總電壓是每個元件上的電壓之和。

以同樣的方式 - 在加法的幫助下 - 也可以找到電路部分的總電阻。你怎麼能想像呢？流過元件鏈的電流依次克服所有電阻。逐個。也就是說，要找到他克服的阻力，需要將阻力相加。或多或少是這樣的。數學推導比較複雜，也比較容易理解這個定律的機理。

並聯

並聯連接是指導體/元件的起點在一個點會聚，而在另一個點連接它們的末端。我們將嘗試解釋對此類化合物有效的定律。讓我們從電流開始。一定量級的電流被提供給元件的連接點。它分離，流經所有導體。由此我們得出結論，該部分的總電流等於每個元件中的電流之和：I = I1 + I2 + I3。

現在是電壓。如果電壓是移動電荷的功，那麼移動一個電荷所需的功在任何元素上都是相同的。也就是說，每個並聯元件上的電壓將相同。 U=U1=U2=U3。不像解釋鏈節的歐姆定律那樣有趣和直觀，但你可以理解。

並聯法則

對於阻力，事情要復雜一些。讓我們介紹一下電導率的概念。該特性表明電荷通過該導體的難易程度。很明顯，電阻越低，電流就越容易通過。因此，電導率 - G - 計算為電阻的倒數。在公式中，它看起來像這樣：G = 1/R。

為什麼我們要談論電導率？因為單元並聯的部分的總電導率等於每個部分的電導率之和。 G = G1 + G2 + G3 - 容易理解。電流將如何輕鬆地克服並聯元件的這個節點取決於每個元件的電導率。所以事實證明它們需要折疊。

現在我們可以繼續抵抗了。由於電導率是電阻的倒數，我們可以得到以下公式：1/R = 1/R1 + 1/R2 + 1/R3。

是什麼給了我們並行和串行連接？

理論知識很好，但如何在實踐中應用呢？任何類型的元件都可以並聯和串聯。但是我們只考慮了描述線性元素的最簡單的公式。線性元件是電阻，也稱為“電阻器”。所以這裡是你如何使用你學到的東西：

如果沒有大阻值電阻可用，但有幾個較小的電阻，則可以通過串聯幾個電阻來獲得所需的電阻。如您所見，這是一種有用的技術。
為了延長電池的壽命，它們可以並聯。根據歐姆定律，這種情況下的電壓將保持不變（您可以通過用萬用表測量電壓來確定）。而且雙電池的“壽命”將比兩個相互替換的元件長得多

請注意：只有具有相同電位的電源才能並聯。也就是說，不能連接一個沒電的電池和一個新的電池。

如果您仍然連接，則電量較大的電池將傾向於為電量較少的電池充電。結果，它們的總電荷將下降到一個較低的值。

一般來說，這些是這些化合物最常見的用途。

理想的 EMF 源

電動勢 (E) 是一個物理量，它決定了外力對電荷載流子閉合電路中運動的影響程度。換句話說，電流流經導體的強度將取決於 EMF。

在解釋這種難以理解的現象時，國內學校教師喜歡求助於水力類比的方法。如果導體是管道，電流是流過它的水量，那麼 EMF 是泵為泵送流體而產生的壓力。

電動勢一詞與電壓等概念有關。她，EMF，也以伏特（單位 - “V”）為單位。每個電源，無論是電池、發電機還是太陽能電池板，都有自己的電動勢。這個 EMF 通常接近輸出電壓 (U)，但總是略低於它。這是由源的內部電阻引起的，這部分電壓不可避免地會下降。

出於這個原因，EMF 的理想來源是一個抽象的概念或物理模型，在現實世界中沒有位置，因為電池 Rin 的內阻雖然非常低，但仍與絕對零不同。

理想和真實的電動勢源

差分形式

該公式經常以微分形式呈現，因為導體通常是不均勻的，因此有必要將其分成盡可能小的部分。通過它的電流與大小和方向有關，因此它被認為是一個標量。每當要找到通過導線的合成電流時，都要取所有單個電流的代數和。由於此規則僅適用於標量，因此電流也被視為標量。已知電流 dI = jdS 通過該段。它上面的電壓是 Edl，那麼對於具有恆定橫截面和相等長度的導線，該比率將為真：

微分形式

因此，矢量形式的電流表達式為：j = E。

重要的！在金屬導體的情況下，電導率隨著溫度的升高而降低，而對於半導體來說，它會增加。奧莫夫定律沒有表現出嚴格的相稱性

一大群金屬和合金的電阻在接近絕對零的溫度下消失，這個過程稱為超導。